最优化-线性规划

基础知识

线性规划的标准形式

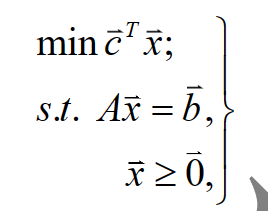
若 A中有m 个列向量可以合并成为单位矩阵，且对应的b>0，此时则称其为线性规划的典范形式

一般形式化为标准形式

松弛变量 <=

剩余变量 >=

自由变量以上要求变量非负自由取值的变量称为自由变量

消除自由变量：

引入x+ x-
取包含x的等式约束

解的性质

凸多面体：有限个半空间的交，凸规划中容许集是凸多面体

凸多边形：有界的凸多面体

基：A（约束矩阵）中m个线性无关的列向量，基中每个列向量称为基向量，基向量组成的矩阵称为基矩阵，由单位向量组成的基矩阵称为标准基，与基向量对应的变量称为基变量

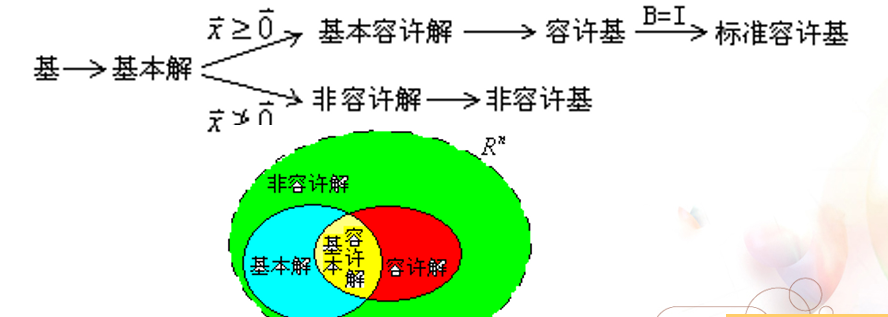
基本：非基变量均为0

容许：变量非负

容许基：基本容许解对应的基，若基是单位矩阵，称为标准容许基

退化：

基变量取值皆不为零的基本容许解称作非退化的，否则称为退化的
若线性规划的所有基本容许解都是非退化的，称为非退化的

单纯形法

基本思想：
首先找到(求出)一个极点(基本容许解) $x_0$ ，并依据最优性准则判断其最优性，如非最优，则沿凸多面体D的一条棱找到(迭代到)使目标值降低(不找比x的目标值高的）的下一个极点(基本容许解) $x_1$ ，极点个数是有限的，所以在一定的条件下，总可以找到(选代到)最优极点(最优基本容许解) 或者说明解无界

最优性判别

设B是一个基,则 $\sigma_j =c_B^TB^{-1}a_j-c_j$ 称为 $x_j$ 关于B的判别数

若所有变量关于基B的判别数都非正,则关于基B的基本容许解是最优解,称B为最优基

求解过程:

求出基对应的基本容许解 $x_{B_1}=B_1^{-1}b$
最优要求所有变量,即 $a_j$ 需要为A,但基变量对应的 $A_B$ 一定是零,只需求 $A_N$ 的判别数
先求 $u=c_B^TB^{-1}$
再逐个求 $\sigma_j =ua_j-c_j$

一般形式的单纯形法

一阶段

这一阶段的目的是将不等式约束变为等式约束,消除人工变量并变为典范形式

$\begin{cases} min:&x_1+x_2+x_3 \\st:& x_1-2x_2+4x_3\leq4\\&4x_1-9x_2-3x_3\leq16 \end{cases}$

由于约束中有不等式,需要将其变为等式,引入人工变量 $u_1,u_2$ :

$x_1-2x_2+4x_3+u_1=4,4x_1-9x_2-3x_3+u_2=16$

此时原式变为以u1u2为基变量的典范形式

列出初始表:

$x_B$	$x_1$	$x_2$	$x_3$	$u_1$	$u_2$	$b$
$u_1$	1	-2	4	1	0	4
$u_2$	4	-9	-3	0	1	16
-c	0	0	0	-1	-1	0
$\sigma$	5	-11	1	0	0	20

前三行照抄即可,注意一阶段的-c是只针对引入的人工变量的c

第四行 $\sigma$ :我们的目的是让基变量的列对应的 $\sigma$ 的值变为0,所以该行由 $u_1+u_2-c$ 得出

每次计算出 $\sigma$ 行后需要进行终止条件判断:

$\sigma$ 行x部分非正,b部分为0,此时基变量中没有人工变量,结束一阶段
$\sigma$ 行x部分非正,b部分为0,此时基变量中有人工变量,但u行x列的a值均为0,结束一阶段,将非人工变量抄下来进行阶段二
$\sigma$ 行x部分非正,b部分为0,此时基变量中有人工变量,u行x列的a值不均为0,继续进基(此时 $\sigma$ 可以为负数,但是不能为0)
$\sigma$ 行x部分非正,b部分不为0,此时无解
$\sigma$ 行x部分有正数,继续进基

现在,显然有两列 $\sigma$ 的值都为正数,此时选取哪一列进基都行(Bland规则后续再讲),注意到x1列的 $a_{11}$ 是1,可能减少后续计算难度,所以选取x1为进基列(第一阶段优先考虑退基人工变量,其次考虑计算难度)

计算比值:b/a 选取最小的作为主元:min(4/1,16/4) 此时a21,a11都可作为主元,但a11计算方便,选取a11作为主元,此时一次迭代完成

$x_1$	1	-2	4	1	0	4
$u_2$	0	-1	-19	-4	1	0

$\sigma$	0	-1	-19	-5	0	0

由于主元a11,所以u1变为x1

$x_{1新}$ = $u_{1旧}/n$ ,其中n是让a主元位置a11变为1的数,由于本身是1,所以不用变

$u_{2新}=u_{2旧}+nx_{1新}$ ,其中n是让u2的进基列对应值(a21)计算后为0的数 u2=u2-4x1

相似地 $\sigma_新=\sigma_旧-5x_{新}$ ,这样达到上次迭代的进基列除上次迭代的主元为1其他均为0的要求

终止条件检测:u行x列不均为0,继续进基,选择a22为主元(此时 $\sigma$ <0也可) 第二次迭代结束

$x_1$	1	0	42	9	-2	4
$x_2$	0	1	19	4	-1	0

$\sigma$	0	0	0	-1	-1	0

x2=-u2 x1=x1+2x2 $\sigma=\sigma+x_2$

第一阶段结束,x1x2作为第二阶段基变量

二阶段

$x_B$	$x_1$	$x_2$	$x_3$	$b$
$x_1$	1	0	42	4
$x_2$	0	1	19	0
-c	-1	-1	-1	0
$\sigma$	0	0	60	4

x1x2抄一阶段的非人工基变量,-c是原式而不是人工变量的c

σ行的目标是让基变量列均为0,σ=x1+x2-c

此时基变量对应的b是最优解,σ对应的b是最优解值

x= $\begin{bmatrix} 4 \\ 0 \\ 0 \\ \end{bmatrix}$ ,z=4,注意最后的解要把非基变量带上

若二阶段中 $\sigma _l >0(不局限为基变量对应列),a_l<0$ 说明解无界

Bland规则

避免循环

进基:正判别数最小下标进基

退基:所有可能的退基向量中,最小下标退基